I’m always on the lookout for more unusual questions about run-of-the-mill mathematics topics.
When finding the area of a rectangle for example, students very often automatically look for the numbers to put into the formula. I was therefore intrigued by the area maze problems created by Japanese mathematician Naoki Inaba, as featured in Alex Bellos’ ‘Monday puzzle’.
These problems ask you to find the missing area, but the use of fractions or decimals isn’t allowed at any point in your solution – whole numbers only!
Solving these problems requires a high level of mathematical reasoning and problem solving skills. Unlike plugging numbers into a formula, it is not obvious where to start or what actions to take.
As a mathematics teacher, my challenge is not only to incorporate these styles of questions into my classroom, but also to consider how to support and build students’ thinking as they approach these types of problems.
Using Geoboards is one way to help. Using resources from the excellent ATM publication ‘Exploring Area and Fractions with Square Geoboards’ we can explore the area of shapes using nine pin Geoboards. The aim of the task is to find the area of the shape in as many different ways as possible given the basic assumption that four pins form a unit square.
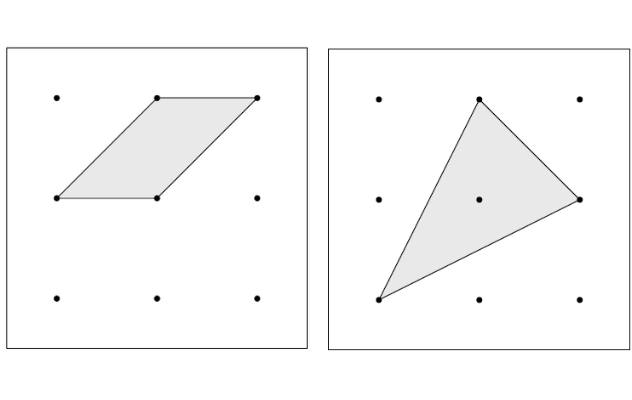
On our residential ‘Using manipulatives to enhance understanding’ CPD, we explore a range of Geoboards tasks. The task below is one of my favourites:
Find the area of the darker shaded area.
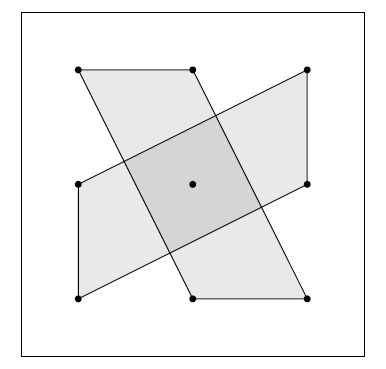
There are a number of different ways of working out an answer. I’ve seen solutions involving coordinates, equations of lines, simultaneous equations and vectors, in addition to standard area formulae - causing a great deal of discussion in the room!
Geoboards can be used for much more than exploring area. Inspired by another ATM publication ‘Exploring Geometry with a 9 Pin Geoboard’ angles in triangles can also be explored using a circular 9 pin Geoboard.
In these two problems the task is simple: find the angles in the triangle. The key is that it is the method employed in which we have interest rather than the answers themselves.
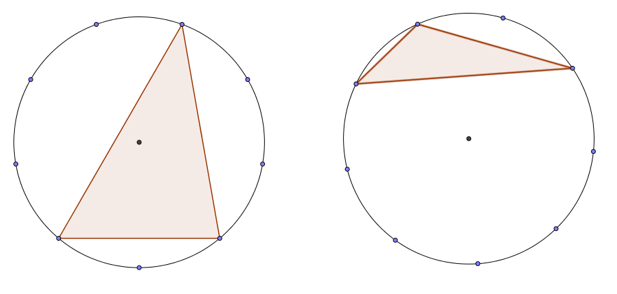
Have a go at the problems above and post your solutions below. If you would like to explore the use of Geoboards and a variety of other manipulatives, join us on our two-day bursary-supported course.
