Recent years have seen a rise in popularity of certain manipulatives, including Cuisenaire rods and algebra tiles, while other manipulatives have a tendency to gather dust in the maths department store cupboard. Dominoes, for example, are often overlooked.
We think it’s time to dust off the dominoes and dive in with these domino-based classroom activities to help deepen students’ mathematical understanding:
1. First things first
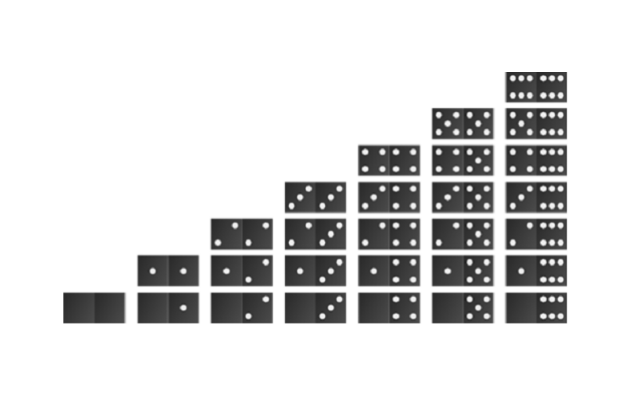
It’s often worth checking if each set is complete before starting. I deliberately remove a domino from each set and ask students to check whether their set is complete, and if not, I ask which domino is missing. This activity gives students the chance to become familiar with the set, look for patterns and work systematically. Arranging the dominos into a ‘stair-case’ pattern leads nicely to a discussion about triangular numbers.
2. Play the game
As with other manipulatives, it is worth dedicating some time for ‘free-play’. Once students have played a traditional game or two, the variation ‘fives and threes’ can be introduced. In this game, if the two ends of the domino chain end in a multiple of three or a multiple of five, the player scores points.
3. Probing questions
Frank Tapson’s ‘Dominoes resource’ contains a wealth of great activities - some of which we explore below, but it also asks some brilliant questions including:
- how many dominoes are there in the double-six set?
- how many doubles are there?
- how many ones, twos or threes etc. are there?
- how many dominoes have a total of ten dots on them?
- how many dominoes have a total of five dots on them?
- how many have an odd total on them?
- how many dominoes are there with a difference of three between the two halves?
- how many dots are there altogether in a complete set?
- what is the greatest/least number of dots to be found on three dominoes?
Often, these questions can lead into others - how many dominoes are in a double-one set? Giving students the opportunity to manipulate the set of dominoes in front of them can often give them confidence to discuss a range of different problem solving strategies.
4. Magic addition squares
If each row and column have to add to the same total, can you complete the following diagrams using only the dominos shown below the diagram?
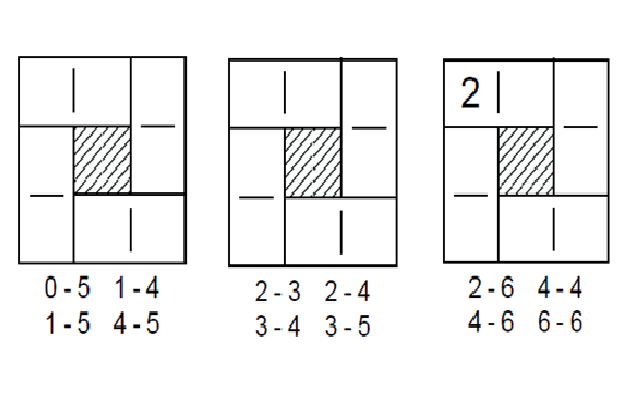
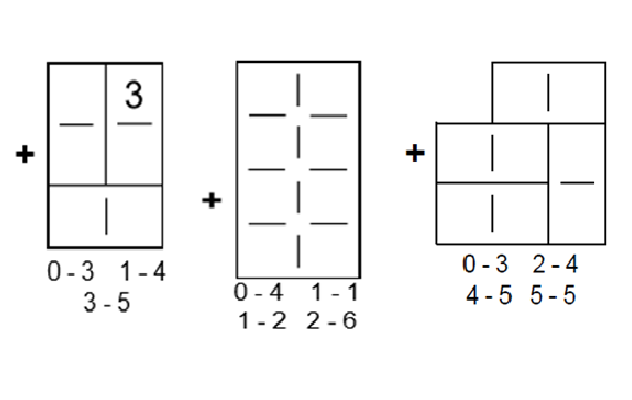
5. Column addition
In the examples above, students rarely have to practice anything other than mental addition. However, the idea can be extended to introduce column addition. The use of dominoes can develop into an engaging experience for students. Can you complete the following additions using only the dominos listed below?
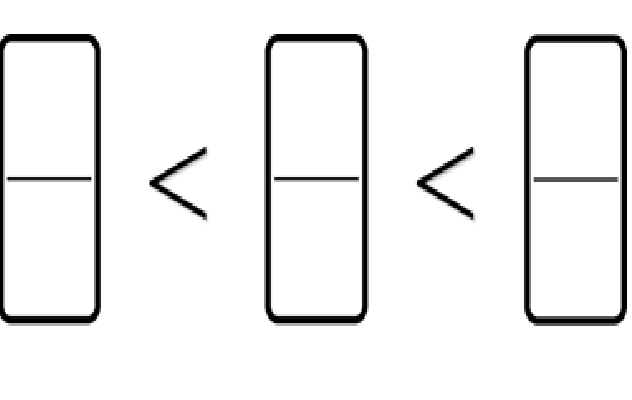
6. Comparing fractions
How many different ways can students complete the diagram below?
Or this one?
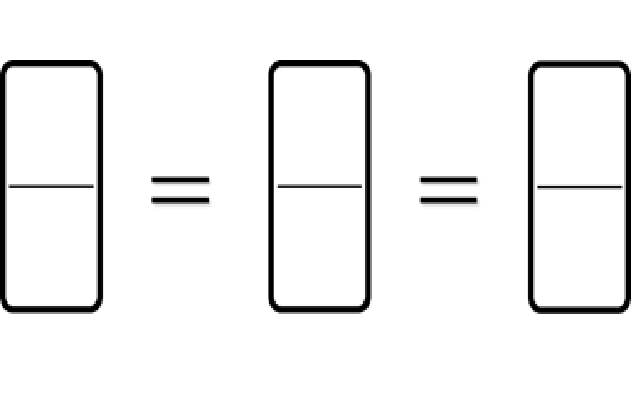
7. Fraction manipulation
Is it possible to get a total of one using the diagrams below? How close can you get to one, without equalling one?
In the examples, what is the largest total that can be made? What is the smallest?
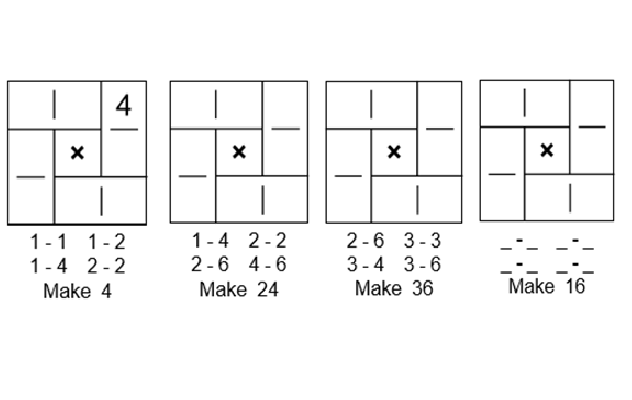
8. Magic multiplication squares
Complete the following so that each row and column make the same number?
Is there more than one way to complete the task? How do you know when you have found all the possible solutions?
9. Domino magic
- pick a domino
- double one of the numbers
- add three to your answer
- multiply your answer by five
- add the other number on the domino
- subtract 15
- what do you notice about your answer?
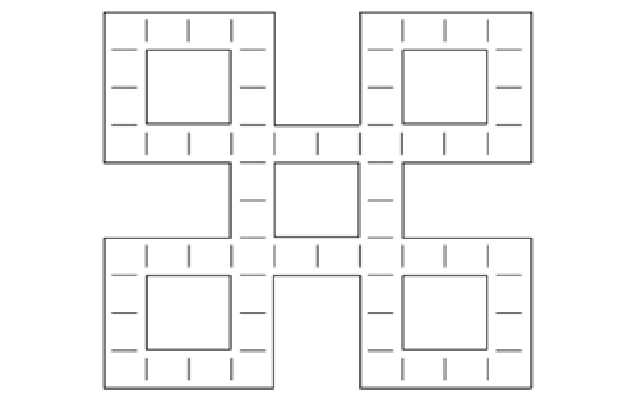
10. Making shapes
If every end has to match, can students complete the domino knot below?
Turning the dominoes so that the spots face down, can students make a rectangle? How many are possible? Can they make squares? Or shapes with rotational or reflectional symmetry?
With the spots facing up, can they make shapes with different orders of symmetry, like the one below with rotational symmetry of order 2?

How do you use dominoes in your classroom? Please share your ideas in the comment section below.
For more ideas on using manipulatives, why not join us at the National STEM Learning Centre on our residential, bursary supported CPD Using manipulatives to enhance understanding in secondary mathematics
You can find a host of classroom domino resources on the STEM Learning site here
